Mohamad Shoumany | Staff Writer

The infamous Monty Hall problem is a mathematical riddle based on simple yet, for some, unintuitive probability analysis. We present it as follows:

You are playing a TV game show. In front of you lie three doors. Behind one of the doors is a car, and the other two have goats behind them. The goal of the game is to guess which door said car is behind. The game show host, let us call him Alan, first asks you to choose the door behind which you think the car is. However, the chances are even; the car is equally likely to be behind any of the three. So, your initial pick is just a guess.

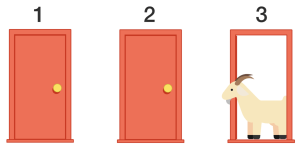
After you make your guess, Alan opens one of the two doors that you did not choose. Specifically, he reveals one which hides a goat. Now, you are left with two closed doors in front of you, one of which is winning (has the car behind it), and the other is losing (has a goat behind it). The twist is that after Alan does reveal a losing door, he gives you the option to switch your pick from your current one to the other unopened door. The question is, do you take his offer, or do you stick with your initial guess?

Logic demands that your decision must be based on whether switching is advantageous, i.e. increases your winning chances or not. With that in mind, you, the reader, are kindly asked to play along with Alan. After your initial guess and Alan’s stipulation, would you switch doors? Many people decide that switching and not switching doors result in the same winning chances, so to them, Alan’s offer doesn’t matter. This line of reasoning goes as follows:

After Alan reveals a losing door, the player is faced with a choice between two doors. Since the game is fair and random, the probability of the car being behind either is equal. It is, in fact, simply a 50% chance for either, like a coin flip. So, the offer is redundant, and sticking with the initial guess does no harm.

However, that is a fundamentally flawed justification. It is not “logical” as much as it is intuitive; it seems to many that a fair game remains fair, and Alan intervening to reveal losing doors is pointless since the real placement of the car remains unknown. Before explaining the correct answer and its probability distribution, let us modify the game in such a way that reveals how this intuition is misleading, using some of the same thinking patterns.

Suppose that instead of three doors, you are asked to choose from a thousand! The same set of rules apply and you take an initial guess of where the car is. After you choose, Alan opens 998 doors to reveal that the car is not behind any of them; they all had goats. He gives you the option to switch to that last remaining unopened door. Would you take it? How confident are you in your initial guess, and in the reasoning behind sticking to it?

If not already apparent, the answer to the absurd proposition above is to switch doors, and it is so in the original game too. To further understand this, we can break down the probabilities of winning and losing at each stage of the game. Initially, since the car is placed randomly behind one of the three doors, the probability of it being behind each is one over three, or 33.3%, and so is the chance of winning To reiterate: since the player gets only one choice of any door, the probability of having picked the right one, i.e., of winning, is also 33.3%. That being the case, the probability of losing is 66.66%, distributed equally among two doors (33.3% for each). Alan then reveals, from among the unchosen doors, one that is losing. The probability of having first chosen the correct door is not affected by Alan’s actions, since those events are independent of each other. 

Thus, the probability of losing is still 66.6%, but now instead of it being distributed among two doors, it is distributed on one, the unopened door that you did not choose. In other words, the chance that the car is in one of the “other” doors was and remains two in three, but Alan’s revelation simply reduces the number of those unopened doors to one. So, Alan is simply asking the player whether they would like to switch their winning and losing chances by switching doors, and the answer must be yes. If switched, the player wins 66.6% of the time.

This logic applies to the thousand doors we talked about previously, if 998 doors are known to contain goats, then there are two doors remaining. Your initial guess, which has a 1% chance of winning and 99% chance of losing, and the other unopened door which solely represents this losing chance. Thus, Switching to it quite literally flips your odds of winning and losing.

Such riddles challenge the human urge to blindly follow what seems right, and if not given enough thought, appear to be simply games of luck.. While the Monty Hall problem is known for its relatively simple and witty solution, creating a “gotcha” moment for the player, it acts as an exposition of some fundamental laws in probability and introduces higher-level concepts. For example, a 66.6% winning chance can be seen in practice by applying the Central Limit Theorem, that is, if one plays the game a thousand times, one will win on an average of 667 times, which reflects the theoretical understanding of the riddle more accurately than playing it only a few times with more volatile results.

Finally, besides being the reason we failed and will fail many exams, Laplace said some enthralling words on probability: 

“The theory of probabilities is at the bottom only common sense reduced to calculation; it makes us appreciate with exactitude what reasonable minds feel by a sort of instinct, often without being able to account for it. … It is remarkable that [this] science, which originated in the consideration of games of chance, should have become the most important object of human knowledge.” –Pierre-Simon Laplace, Philosophical Essay on Probabilities (1814), 5th edition (1825), trans. Andrew I. Dale (1995), 124.

Sources:

todayinsci.com/L/Laplace_Pierre/LaplacePierre-Probability-Quotations.htm#:~:text=The%20theory%20of%20probabilities%20is%20at%20bottom%20only.

Central limit Theorem: en.wikipedia.org/wiki/Central_limit_theorem.